3 Divided By 3 4
disgrace
Sep 25, 2025 · 5 min read
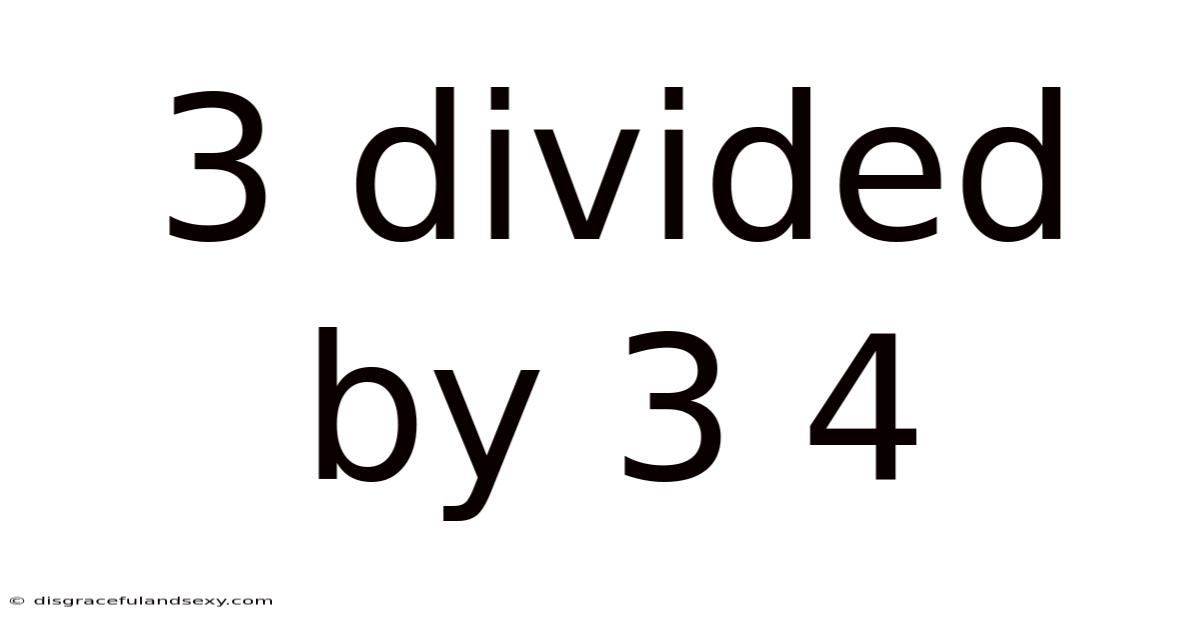
Table of Contents
Unpacking the Mystery: 3 Divided by 3/4
Understanding fractions and division can sometimes feel like navigating a mathematical maze. This article aims to demystify the seemingly simple, yet often confusing, calculation of 3 divided by 3/4 (3 ÷ ¾). We'll explore the problem step-by-step, providing a clear explanation suitable for anyone from middle school students to adults looking to refresh their math skills. We’ll delve into the underlying principles, offer alternative approaches, and address frequently asked questions to ensure a comprehensive understanding of this fundamental arithmetic operation.
Introduction: Why This Calculation Matters
The calculation 3 ÷ ¾ might seem trivial at first glance. However, mastering this type of problem is crucial for building a solid foundation in arithmetic. Understanding how to divide by fractions is essential for various applications, from baking (adjusting recipes) to construction (calculating materials) and beyond. This seemingly simple calculation underscores a core concept in mathematics: the reciprocal and its application in division.
Understanding the Basics: Division and Reciprocals
Before diving into the specific calculation, let's review some key concepts. Division is essentially the inverse operation of multiplication. When we divide one number by another, we're asking, "How many times does the second number fit into the first number?"
A reciprocal (also known as the multiplicative inverse) of a number is the value that, when multiplied by the original number, equals 1. For example, the reciprocal of 2 is ½ (because 2 x ½ = 1), and the reciprocal of ¾ is 4/3 (because ¾ x 4/3 = 1).
Method 1: The "Keep, Change, Flip" Method
This popular method offers a simple, three-step process for dividing fractions:
-
Keep: Keep the first number (the dividend) as it is. In our case, this remains 3.
-
Change: Change the division sign (÷) to a multiplication sign (x).
-
Flip: Flip the second number (the divisor) – find its reciprocal. The reciprocal of ¾ is 4/3.
Therefore, 3 ÷ ¾ becomes 3 x 4/3.
Now, we simply multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(3 x 4) / (1 x 3) = 12/3
Finally, we simplify the fraction: 12/3 = 4
Therefore, 3 divided by ¾ equals 4.
Method 2: Converting to a Common Denominator
This method emphasizes the conceptual understanding of division. We can rewrite the whole number 3 as a fraction with a denominator of 4 (to match the divisor):
3 = 12/4
Now, our division problem becomes: (12/4) ÷ (3/4)
When dividing fractions with a common denominator, we simply divide the numerators:
12 ÷ 3 = 4
This method directly showcases how many times 3/4 "fits" into 12/4.
Method 3: Visual Representation
A visual approach can further solidify understanding. Imagine you have 3 whole pies. Each pie is divided into four equal slices (quarters). The question "3 ÷ ¾" asks how many sets of three-quarters of a pie you can make from your three whole pies.
By counting the quarter slices, you'll find you can create four sets of three-quarters. This visually confirms our answer of 4.
Explaining the Mathematics: A Deeper Dive
The "Keep, Change, Flip" method isn't just a trick; it's a direct consequence of the properties of fractions and division. When we divide by a fraction, we're essentially multiplying by its reciprocal. This can be explained using the principle of multiplicative inverses and the identity property of multiplication (any number multiplied by 1 equals itself).
Consider the expression a ÷ (b/c). We can rewrite this as:
a x (c/b)
This is because dividing by a fraction (b/c) is equivalent to multiplying by its reciprocal (c/b). This is a fundamental property of fractions and rational numbers. Applying this to our problem:
3 ÷ (3/4) = 3 x (4/3) = 12/3 = 4
Addressing Common Mistakes and Misconceptions
One frequent error is incorrectly multiplying the numerators and denominators without flipping the second fraction. This leads to an incorrect result. Remember, dividing by a fraction is the same as multiplying by its reciprocal. Always flip the fraction you are dividing by.
Another misconception stems from confusing division with subtraction. While both operations involve separating quantities, division involves repeated subtraction until zero is reached or a remainder is found, whereas the fraction represents a part of a whole.
Frequently Asked Questions (FAQ)
-
What if the numbers were different? The methods described here work for any division problem involving fractions and whole numbers. Simply follow the steps, and always remember to find the reciprocal of the divisor.
-
Can I use a calculator? Yes, calculators can efficiently handle fraction division. However, understanding the underlying principles is more important than relying solely on a calculator.
-
Why is understanding this important? Mastering fraction division is fundamental for further mathematical concepts, such as algebra, geometry, and calculus. It's a building block for more complex problem-solving.
-
What are some real-world applications of this skill? Many real-world scenarios require dividing by fractions. Examples include adjusting cooking recipes, calculating the amount of materials needed for a construction project, or determining the unit cost of goods when prices are given in fractions.
-
How can I practice this skill? Practice is key! Try different combinations of whole numbers and fractions. Start with simple examples and gradually increase the complexity. Online resources and math textbooks offer plenty of practice problems.
Conclusion: Mastering Fraction Division – A Stepping Stone to Success
Understanding how to divide by fractions, as exemplified by the calculation 3 ÷ ¾, is a crucial stepping stone in mastering mathematics. By grasping the fundamental concepts of reciprocals and the "Keep, Change, Flip" method, you can confidently tackle this type of problem and build a strong mathematical foundation. Whether you utilize visual aids, convert to common denominators, or rely on the established methods, the key lies in understanding the underlying mathematical principles. Continue practicing, and you'll soon find fraction division as intuitive as other arithmetic operations. Don't be afraid to explore different approaches – the more you understand the "why" behind the "how," the stronger your mathematical foundation will become. The journey through numbers may seem challenging at times, but with persistence and understanding, you can confidently conquer any mathematical obstacle.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.