8 12 In Simplest Form
disgrace
Sep 25, 2025 · 6 min read
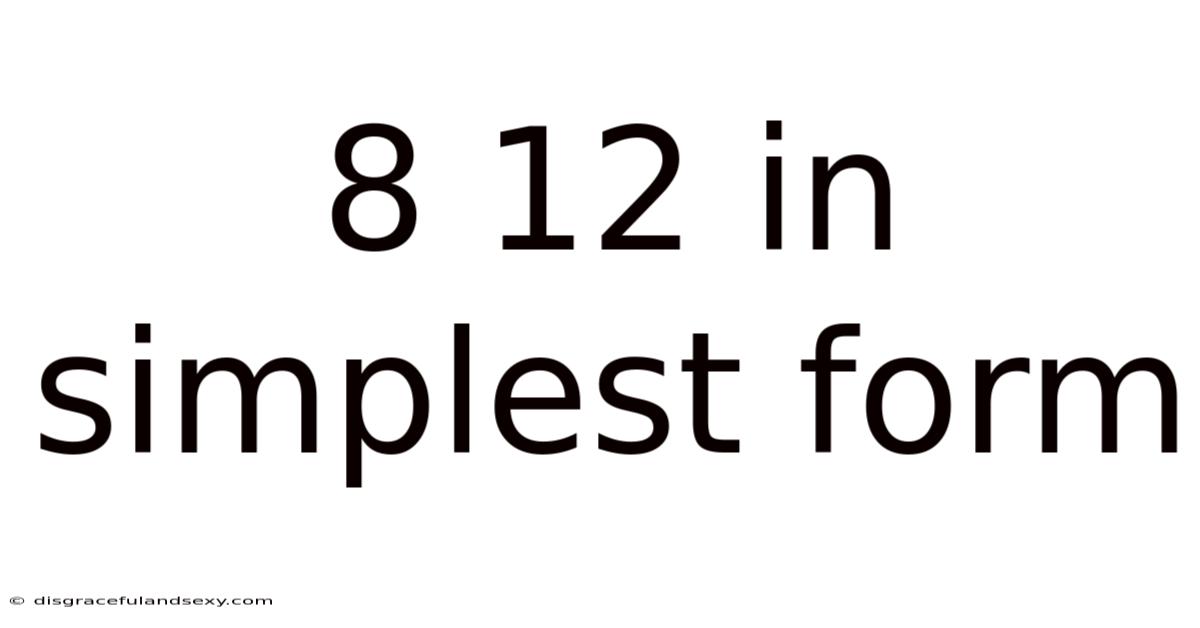
Table of Contents
Simplifying Fractions: Understanding 8/12 in its Simplest Form
Understanding fractions is a fundamental skill in mathematics, forming the building blocks for more advanced concepts. This article will delve into the process of simplifying fractions, using the example of 8/12 to illustrate the method and provide a deeper understanding of the underlying principles. We'll explore the concept of greatest common divisors (GCD), explain why simplification is important, and answer frequently asked questions to solidify your comprehension. By the end, you'll be confident in simplifying any fraction and grasp the importance of expressing fractions in their simplest form.
What is a Fraction? A Quick Recap
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 8/12, 8 is the numerator and 12 is the denominator. This means we have 8 parts out of a total of 12 equal parts.
Why Simplify Fractions?
Simplifying fractions, also known as reducing fractions, means finding an equivalent fraction with a smaller numerator and denominator. While 8/12 is a perfectly valid representation, it's not in its simplest form. Simplifying fractions offers several advantages:
- Clarity: Simpler fractions are easier to understand and visualize. It's much clearer to grasp the concept of 2/3 than 8/12, even though they represent the same value.
- Easier Calculations: Simplifying fractions makes subsequent calculations, such as addition, subtraction, multiplication, and division, much simpler and less prone to errors.
- Standardized Representation: Expressing fractions in their simplest form ensures a consistent and universally understood representation of a numerical value.
How to Simplify 8/12: A Step-by-Step Guide
The key to simplifying fractions lies in finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Let's find the simplest form of 8/12:
Step 1: Find the Factors of the Numerator (8)
The factors of 8 are the numbers that divide 8 evenly: 1, 2, 4, and 8.
Step 2: Find the Factors of the Denominator (12)
The factors of 12 are: 1, 2, 3, 4, 6, and 12.
Step 3: Identify the Greatest Common Divisor (GCD)
Comparing the lists of factors, we see that the largest number that appears in both lists is 4. Therefore, the GCD of 8 and 12 is 4.
Step 4: Divide Both the Numerator and the Denominator by the GCD
Now, we divide both the numerator (8) and the denominator (12) by the GCD (4):
8 ÷ 4 = 2 12 ÷ 4 = 3
Step 5: The Simplified Fraction
This gives us the simplified fraction: 2/3. Therefore, 8/12 in its simplest form is 2/3.
Alternative Methods for Finding the GCD
While listing factors works well for smaller numbers, it can become cumbersome with larger numbers. Here are two alternative methods for finding the GCD:
-
Prime Factorization: This method involves breaking down the numerator and denominator into their prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
For example:
8 = 2 x 2 x 2 = 2³ 12 = 2 x 2 x 3 = 2² x 3
The common prime factor is 2, and the lowest power is 2². Therefore, the GCD is 2² = 4.
-
Euclidean Algorithm: This is an efficient algorithm, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Let's apply the Euclidean algorithm to 8 and 12:
12 ÷ 8 = 1 with a remainder of 4 8 ÷ 4 = 2 with a remainder of 0
The last non-zero remainder is 4, so the GCD is 4.
Visual Representation of 8/12 and 2/3
Imagine a pizza cut into 12 slices. 8/12 represents having 8 out of those 12 slices. If you group those 8 slices into groups of 4, you'll have 2 groups. Similarly, if you divide the entire pizza into 3 equal parts (each part consisting of 4 slices), then 2/3 represents having 2 out of those 3 parts. Both 8/12 and 2/3 represent the same amount of pizza.
Further Examples of Fraction Simplification
Let's practice with a few more examples:
- 15/25: The GCD of 15 and 25 is 5. 15 ÷ 5 = 3 and 25 ÷ 5 = 5. Therefore, 15/25 simplifies to 3/5.
- 18/24: The GCD of 18 and 24 is 6. 18 ÷ 6 = 3 and 24 ÷ 6 = 4. Therefore, 18/24 simplifies to 3/4.
- 21/35: The GCD of 21 and 35 is 7. 21 ÷ 7 = 3 and 35 ÷ 7 = 5. Therefore, 21/35 simplifies to 3/5.
Improper Fractions and Mixed Numbers
Sometimes, you might encounter improper fractions, where the numerator is larger than the denominator (e.g., 14/3). These can be converted into mixed numbers, which combine a whole number and a fraction (e.g., 4 ⅔). While simplification applies to both improper fractions and mixed numbers, it's typically applied to the fractional part of the mixed number.
Frequently Asked Questions (FAQ)
Q1: What if the GCD is 1?
A1: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. This means the numerator and denominator share no common factors other than 1.
Q2: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
A2: No, to maintain the value of the fraction, you must divide both the numerator and the denominator by the same number (the GCD). Dividing by different numbers will change the value of the fraction.
Q3: Is there a quick way to tell if a fraction is in its simplest form?
A3: A quick check is to see if the numerator and denominator are both prime numbers or if they share no common factors other than 1. However, the most reliable method is to find the GCD.
Q4: Why is simplifying fractions important in real-world applications?
A4: Simplifying fractions is crucial in various real-world applications, including cooking (measuring ingredients), construction (measuring materials), and finance (calculating proportions). Accurate and simplified calculations ensure precise results and prevent errors.
Conclusion
Simplifying fractions is a fundamental skill in mathematics with practical applications in numerous fields. By understanding the concept of the greatest common divisor and applying the methods outlined above, you can confidently simplify any fraction and represent numerical values in their clearest and most efficient form. Remember that practice is key; the more you work with fractions, the more proficient you'll become in simplifying them quickly and accurately. Mastering this skill will significantly improve your mathematical understanding and problem-solving abilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about 8 12 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.