Exact Value Of Sin 165
disgrace
Sep 25, 2025 · 6 min read
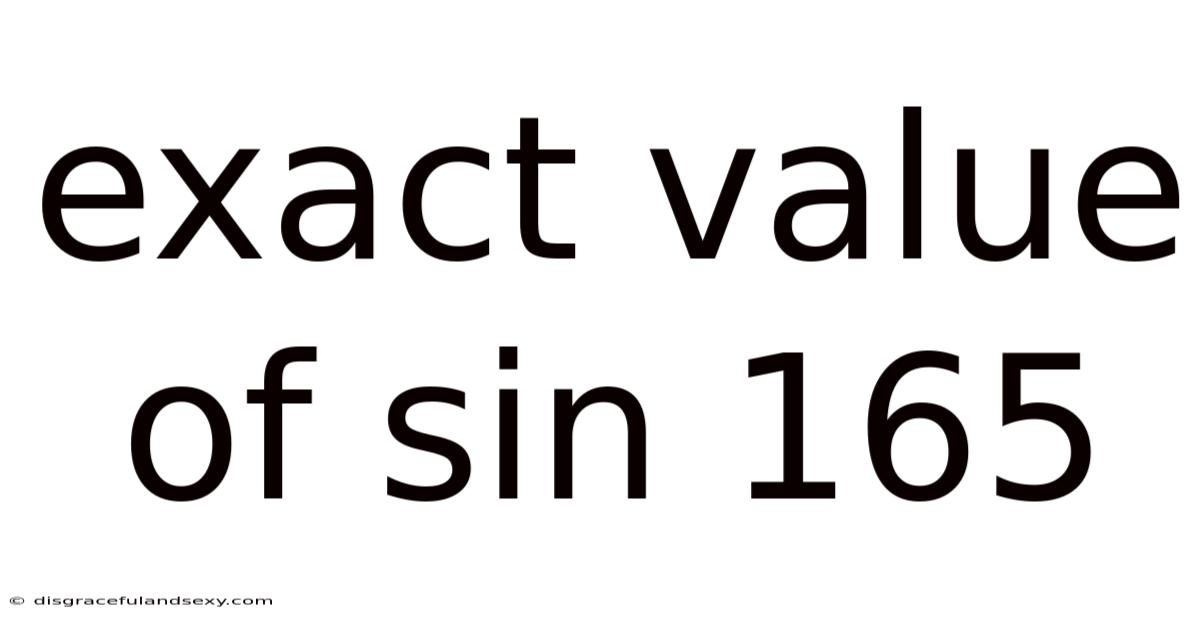
Table of Contents
Unveiling the Exact Value of sin 165°: A Trigonometric Journey
Determining the exact value of trigonometric functions like sin 165° might seem daunting at first, but with the right approach and understanding of trigonometric identities, it becomes a manageable and even rewarding exercise. This article will guide you through a comprehensive exploration of how to find the exact value of sin 165°, not just providing the answer, but also building your understanding of fundamental trigonometric principles. This journey will involve utilizing angle sum and difference formulas, understanding reference angles, and applying unit circle concepts. By the end, you'll be equipped to tackle similar trigonometric challenges with confidence.
Introduction: Why is Finding the Exact Value Important?
In many mathematical and scientific fields, approximations are simply not sufficient. Precision is paramount. While calculators provide approximate values for trigonometric functions, knowing how to derive the exact value is crucial for several reasons:
- Understanding Fundamental Principles: The process reinforces your understanding of core trigonometric identities and relationships.
- Algebraic Manipulation Skills: Solving for exact values hones your algebraic manipulation skills, essential in various mathematical contexts.
- Accuracy in Calculations: Using exact values ensures greater accuracy in complex calculations where accumulated rounding errors can significantly affect the final result.
- Theoretical Rigor: In advanced mathematics and physics, exact values are necessary for theoretical analysis and proofs.
Therefore, understanding the methodology behind finding the exact value of sin 165° is as important, if not more so, than the answer itself.
Method 1: Using the Angle Sum Formula
We can express 165° as the sum of two angles with known trigonometric values. Specifically, 165° = 120° + 45°. This allows us to employ the angle sum formula for sine:
sin(A + B) = sin A cos B + cos A sin B
Let A = 120° and B = 45°. We know the values for sine and cosine of these angles:
- sin 120° = √3/2
- cos 120° = -1/2
- sin 45° = √2/2
- cos 45° = √2/2
Substituting these values into the angle sum formula:
sin 165° = sin (120° + 45°) = sin 120° cos 45° + cos 120° sin 45°
sin 165° = (√3/2)(√2/2) + (-1/2)(√2/2)
sin 165° = (√6/4) - (√2/4)
Therefore, the exact value of sin 165° is (√6 - √2)/4.
Method 2: Using the Angle Difference Formula
Alternatively, we can express 165° as the difference between two angles with known trigonometric values. For instance, 165° = 210° - 45°. Here, we utilize the angle difference formula for sine:
sin(A - B) = sin A cos B - cos A sin B
Let A = 210° and B = 45°. Again, we have:
- sin 210° = -1/2
- cos 210° = -√3/2
- sin 45° = √2/2
- cos 45° = √2/2
Substituting into the angle difference formula:
sin 165° = sin (210° - 45°) = sin 210° cos 45° - cos 210° sin 45°
sin 165° = (-1/2)(√2/2) - (-√3/2)(√2/2)
sin 165° = (-√2/4) + (√6/4)
This simplifies to the same exact value as before: (√6 - √2)/4.
Method 3: Utilizing the Unit Circle
The unit circle provides a powerful visual representation of trigonometric functions. 165° lies in the second quadrant, where sine is positive. We can find a reference angle by subtracting 165° from 180°: 180° - 165° = 15°. The sine of 15° is the same as the sine of 165°, but we need to consider the sign. Since 165° is in the second quadrant, sin 165° is positive.
Finding the exact value of sin 15° can be done using the half-angle formula or by expressing 15° as 45° - 30° and applying the angle difference formula as shown previously.
Regardless of the approach, the result will be the same: (√6 - √2)/4.
A Deeper Dive: Reference Angles and Quadrants
Understanding reference angles is crucial for solving trigonometric problems. A reference angle is the acute angle formed between the terminal side of an angle and the x-axis. It helps simplify calculations because the trigonometric functions of an angle and its reference angle have the same absolute value. The sign depends solely on the quadrant in which the angle lies.
- Quadrant I (0° - 90°): All trigonometric functions are positive.
- Quadrant II (90° - 180°): Only sine is positive.
- Quadrant III (180° - 270°): Only tangent is positive.
- Quadrant IV (270° - 360°): Only cosine is positive.
By identifying the quadrant and the reference angle, we can easily determine the sign of the trigonometric function. This significantly simplifies the process of finding exact values.
Explaining the Result: Why (√6 - √2)/4?
The result (√6 - √2)/4 might seem unusual, but it's a direct consequence of the algebraic manipulation involved in applying the angle sum or difference formulas and the known values of sine and cosine for 45° and 120° (or their equivalents). It's a testament to the interconnectedness of trigonometric identities. This precise value reflects the intricate geometrical relationships within the unit circle.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to verify the answer? A: While you can use a calculator to obtain an approximate value, remember that this will only be an approximation. The goal here is to find the exact value, expressed in radical form.
-
Q: Are there other methods to find sin 165°? A: Yes, other methods involve using half-angle formulas or various other trigonometric identities, but the methods described above are among the most straightforward.
-
Q: Why is it important to learn these methods? A: These methods are fundamental for building a strong foundation in trigonometry and for solving more complex problems in mathematics, physics, and engineering. The ability to manipulate trigonometric identities is an invaluable skill.
-
Q: What if the angle was different, say sin 255°? A: You would follow a similar process, expressing 255° as a sum or difference of angles with known trigonometric values (e.g., 180° + 75°, 210° + 45°, etc.) and then apply the relevant trigonometric identities.
-
Q: Can I use this method for other trigonometric functions like cosine or tangent? A: Yes, absolutely! The same principles apply, but you would use the corresponding angle sum/difference formulas for cosine or tangent instead.
Conclusion: Mastering Trigonometric Identities
Finding the exact value of sin 165° is more than just a numerical exercise; it's a journey into the heart of trigonometry. By mastering the techniques outlined – using angle sum/difference formulas, understanding reference angles and quadrants, and leveraging the unit circle – you equip yourself with powerful tools for tackling a wide range of trigonometric problems. The seemingly complex result, (√6 - √2)/4, is a testament to the beautiful precision and underlying mathematical elegance inherent in trigonometry. Remember, the journey of understanding is just as crucial as the destination, so embrace the process and enjoy the intellectual stimulation of uncovering the exact value of trigonometric functions. This knowledge will serve as a strong foundation for further exploration in mathematics and related fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Exact Value Of Sin 165 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.